Week 12: Actor-Critic 方法

回顾：策略梯度 (Policy Gradient) 与 REINFORCE

上周我们学习了策略梯度 (PG) 方法：

• 核心思想: 直接参数化策略 \(\pi(a|s, \theta)\) 并优化参数 \(\theta\) 以最大化预期回报 \(J(\theta)\)。
• 优化方式: 梯度上升 \(\theta \leftarrow \theta + \alpha \nabla J(\theta)\)。
• 策略梯度定理: \(\nabla J(\theta) = E_{\pi_{\theta}} [ \nabla \log \pi(A_t|S_t, \theta) * Q_{\pi}(S_t, A_t) ]\) (或使用 \(G_t\))。
• REINFORCE 算法: 使用蒙特卡洛方法估计 \(Q_{\pi}\) (即使用完整回报 \(G_t\))。
  • \(\nabla J(\theta) \approx E_{\pi_{\theta}} [ \nabla \log \pi(A_t|S_t, \theta) * G_t ]\)
  • 缺点: 高方差，收敛慢，需要完整回合。
• 基线 (Baseline): 为了减小方差，从回报中减去一个与动作无关的基线 \(b(S_t)\)。
  • \(\nabla J(\theta) \approx E_{\pi_{\theta}} [ \nabla \log \pi(A_t|S_t, \theta) * (G_t - b(S_t)) ]\)
  • 常用的基线是状态值函数 \(V_{\pi}(S_t)\)。
  • 优势函数 (Advantage Function): \(A_{\pi}(S_t, A_t) = Q_{\pi}(S_t, A_t) - V_{\pi}(S_t)\)。
  • 梯度变为：\(\nabla J(\theta) = E_{\pi_{\theta}} [ \nabla \log \pi(A_t|S_t, \theta) * A_{\pi}(S_t, A_t) ]\)

问题: 如何在不知道 \(Q_{\pi}\) 和 \(V_{\pi}\) 的情况下，有效地估计优势函数 \(A_{\pi}\) 并进行策略更新？

Actor-Critic 框架

Actor-Critic (AC) 方法提供了一个优雅的解决方案，它结合了策略梯度和TD学习的思想。

核心思想: 维护两个参数化的模型（通常是神经网络）：

1. Actor (行动者):
   • 参数化的策略 \(\pi(a|s, \theta)\)。
   • 负责根据当前状态 \(s\) 选择动作 \(a\)。
   • 目标是优化参数 \(\theta\) 以改进策略。
2. Critic (评论家):
   • 参数化的价值函数（通常是状态值函数 \(V(s, w)\) 或动作值函数 \(Q(s, a, w)\)）。
   • 负责评估 Actor 选择的动作有多好。
   • 目标是学习准确的价值估计，参数为 \(w\)。

交互流程:

1. Actor 根据当前状态 \(S_t\) 和策略 \(\pi(·|·, \theta)\) 选择动作 \(A_t\)。
2. 执行动作 \(A_t\)，观察到奖励 \(R_{t+1}\) 和下一个状态 \(S_{t+1}\)。
3. Critic 利用这个转移 \((S_t, A_t, R_{t+1}, S_{t+1})\) 来评估动作 \(A_t\) 的好坏，并更新其价值函数参数 \(w\)。
4. Actor 利用 Critic 的评估信息来更新其策略参数 \(\theta\)。

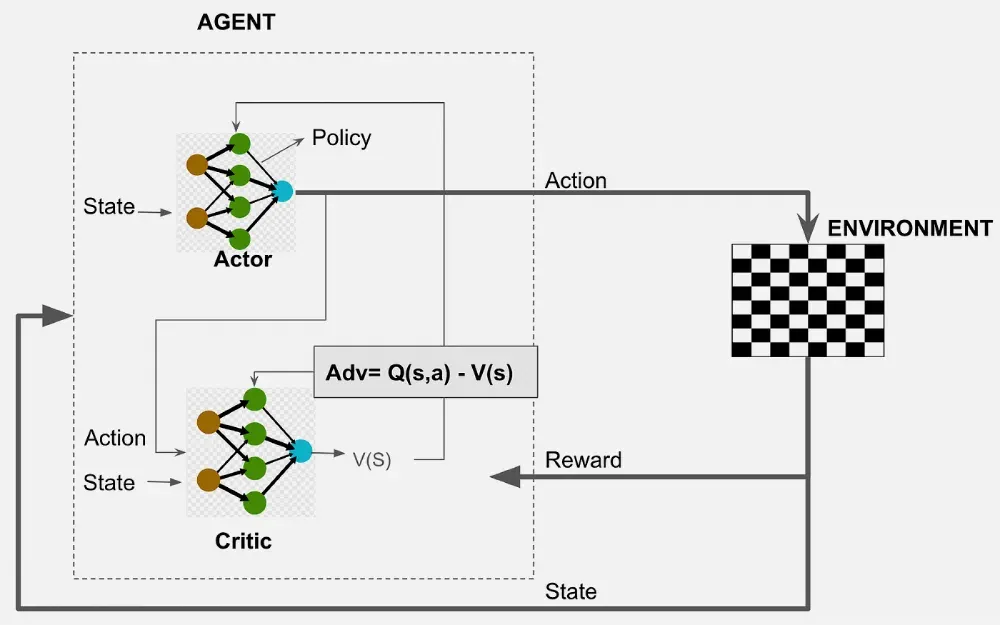(图片来源: https://www.geeksforgeeks.org/actor-critic-algorithm-in-reinforcement-learning)

Critic 如何帮助 Actor？

Critic 的主要作用是提供一个比蒙特卡洛回报 \(G_t\) 方差更低的信号来指导 Actor 的学习。这通常通过以下方式实现：

• 计算 TD 误差: 如果 Critic 学习的是状态值函数 \(V(s, w)\)，它可以计算 TD 误差：
  • \(\delta_t = R_{t+1} + \gamma V(S_{t+1}, w) - V(S_t, w)\)
  • 这个 TD 误差 \(\delta_t\) 可以作为优势函数 \(A_{\pi}(S_t, A_t)\) 的一个（有偏但低方差的）估计。
• 更新 Actor: Actor 使用这个 TD 误差来更新策略参数 \(\theta\)：
  • \(\theta \leftarrow \theta + \alpha * \nabla \log \pi(A_t|S_t, \theta) * \delta_t\)
  • 直观理解:
    • 如果 \(\delta_t > 0\) (实际回报 \(R_{t+1} + \gamma V(S')\) 比当前预期 \(V(S)\) 要好)，说明动作 \(A_t\) 是个好动作，增加其概率。
    • 如果 \(\delta_t < 0\) (实际回报比预期差)，说明动作 \(A_t\) 是个坏动作，减小其概率。
• 更新 Critic: Critic 也需要学习，通常使用 TD 学习来更新其参数 \(w\)，目标是最小化 TD 误差（使其对 \(V_{\pi}\) 的估计更准确）：
  • \(w \leftarrow w + \beta * \delta_t * \nabla V(S_t, w)\) (\(\beta\) 是 Critic 的学习率)

为什么 TD 误差是优势函数的估计?

TD 误差 \(\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\) 可以作为优势函数 \(A_{\pi}(S_t, A_t)\) 的估计，原因如下：

1. 数学期望关系:
   • 优势函数定义为 \(A_{\pi}(s,a) = Q_{\pi}(s,a) - V_{\pi}(s)\)
   • TD 误差的期望满足: \(E_{\pi}[\delta_t | S_t, A_t] = Q_{\pi}(S_t, A_t) - V_{\pi}(S_t) = A_{\pi}(S_t, A_t)\)
2. 直观理解:
   • \(R_{t+1} + \gamma V(S_{t+1})\) 是 \(Q_{\pi}(S_t, A_t)\) 的采样估计
   • 减去 \(V(S_t)\) 后，\(\delta_t\) 衡量了”实际获得的回报”与”状态平均价值”的差异
   • 正值表示动作比平均好，负值表示比平均差
3. 实际优势:
   • 相比蒙特卡洛回报 \(G_t\)，TD误差方差更低
   • 不需要等待回合结束，支持在线学习
   • 计算简单，只需一步转移 \((S_t,A_t,R_{t+1},S_{t+1})\)

Actor-Critic 方法的优势

• 结合策略梯度与TD学习: 巧妙融合了策略梯度(PG)的直接策略优化能力和TD学习的低方差优势，有效改善了传统REINFORCE算法的高方差问题。
• 训练更稳定高效: 相比蒙特卡洛式的REINFORCE算法，通常具有更快的收敛速度和更稳定的训练过程。

A2C / A3C 算法概念

A2C (Advantage Actor-Critic):

• 这是 Actor-Critic 的一个同步 (Synchronous)、确定性 (Deterministic) 版本，其概念与 A3C (由 Mnih 等人于 2016 年提出) 紧密相连。
• 通常使用多个并行的环境实例来收集经验数据。
• 智能体在所有环境中执行一步，收集一批 (S, A, R, S’) 数据。
• 使用这批数据计算 TD 误差 δ 和梯度，然后一次性更新 Actor 和 Critic 的参数。
• 由于是同步更新，实现相对简单。Stable Baselines3 中的 A2C 实现的就是这种思想。

A3C (Asynchronous Advantage Actor-Critic):

• 这是 Actor-Critic 的一个异步 (Asynchronous) 版本，由 Mnih 等人于 2016 年在论文《Asynchronous Methods for Deep Reinforcement Learning》中首次提出，是早期深度强化学习 (DRL) 的一个重要里程碑式算法。
• 核心思想: 创建多个并行的 Actor-Learner 线程，每个线程都有自己的环境副本和模型参数副本。
• 每个线程独立地与环境交互，计算梯度（Actor 和 Critic 的梯度）。
• 异步更新: 各个线程独立地、异步地将计算出的梯度应用到全局共享的模型参数上。
• 优点: 不需要经验回放缓冲区（异步性本身提供了数据去相关性）；通过并行化提高了训练速度。
• 缺点: 实现相对复杂；异步更新可能导致某些线程使用过时的参数进行计算。

A2C vs. A3C 实践对比

研究表明，A2C（同步并行版本）在大多数实际任务中表现优于A3C，主要体现在： 1. 性能更优：同步更新机制使训练更稳定，通常能获得更高的最终回报 2. 实现简单：避免了异步更新的复杂性和潜在参数冲突 3. 复现性强：确定性更新过程确保实验结果可重复 4. 资源利用率高：能更好地利用现代GPU的并行计算能力

因此主流框架(如Stable Baselines3)优先支持A2C实现，A3C更多具有历史研究价值。

其他 Actor-Critic 变体与发展

A2C 和 A3C 是 Actor-Critic 思想的重要实现，奠定了基础。在此之后，研究者们提出了许多更先进和性能更强的 Actor-Critic 变体：

• DDPG (Deep Deterministic Policy Gradient): 专门为连续动作空间设计。Actor 输出确定的动作（而不是概率分布），Critic 学习 Q(s,a)。结合了 DQN 中经验回放和目标网络等技巧。
• TRPO (Trust Region Policy Optimization): 旨在通过限制每次策略更新的幅度（在“信任区域”内进行优化）来保证策略的单调改进，从而提高训练的稳定性。
• PPO (Proximal Policy Optimization): TRPO 的一种简化版本，通过裁剪目标函数或使用 KL 散度惩罚项来实现类似 TRPO 的稳定更新效果，但实现更简单，计算效率更高。PPO 目前是许多应用中非常流行且效果出色的算法。
• SAC (Soft Actor-Critic): 一种基于最大熵强化学习框架的 Actor-Critic 算法。它在最大化累积回报的同时，也最大化策略的熵，从而鼓励探索，并能学习到更鲁棒的策略。SAC 在许多连续控制任务上取得了顶尖的性能。
• TD3 (Twin Delayed Deep Deterministic Policy Gradient): DDPG 的改进版本，通过使用两个 Critic 网络（取较小值）、延迟策略更新和目标策略平滑等技巧来缓解 Q 值过高估计的问题，从而提升了 DDPG 的性能和稳定性。

后续发展:

强化学习领域仍然在飞速发展。虽然 PPO 和 SAC 等算法在很多任务上表现优异，但研究者们仍在不断探索新的架构、优化方法和理论，例如：

• 基于模型的强化学习 (Model-Based RL): 学习环境模型，然后利用模型进行规划或生成模拟经验。
• 离线强化学习 (Offline RL): 从固定的数据集中学习策略，而无需与环境进行新的交互。
• 多智能体强化学习 (Multi-Agent RL): 多个智能体在共享环境中学习和交互。
• 与大型语言模型 (LLM) 的结合: 探索如何利用 LLM 的知识和推理能力来增强 RL 智能体的学习和决策。

因此，虽然 A2C/A3C 是重要的里程碑，但后续的 PPO、SAC 等算法在性能和稳定性上通常有更佳表现，并且整个领域仍在不断涌现更为突破性的思想和算法。

Lab 7: 使用 Stable Baselines3 运行 A2C

目标

1. 使用 Stable Baselines3 (SB3) 运行 A2C 算法。
2. 在 CartPole (离散动作) 或 Pendulum (连续动作) 环境上进行实验。
3. 对比 A2C 和 DQN (在 CartPole 上) 的训练过程和结果。
4. 理解 Actor-Critic 方法相对于 DQN 的优势（尤其是在处理连续动作空间方面）。

环境选择

• CartPole-v1: 离散动作空间。可以与上周的 DQN 进行直接比较。
• Pendulum-v1: 连续动作空间。
  • 目标: 通过施加力矩，将倒立摆摆动到最高点并保持稳定。
  • 状态: [cos(杆角度), sin(杆角度), 杆角速度] (连续)。
  • 动作: 施加的力矩 (连续值，通常在 [-2.0, 2.0] 之间)。
  • 奖励: 与杆子角度和角速度有关，目标是最大化奖励（最小化“成本”）。
  • 注意: DQN 无法直接处理 Pendulum 的连续动作空间，而 A2C 可以。

示例代码 (SB3 A2C on CartPole)

import gymnasium as gym
from stable_baselines3 import A2C
from stable_baselines3.common.env_util import make_vec_env
from stable_baselines3.common.evaluation import evaluate_policy
import time
import os

# 创建日志目录
log_dir = "/tmp/gym_a2c/"
os.makedirs(log_dir, exist_ok=True)

# 1. 创建环境 (A2C 通常需要向量化环境)
vec_env = make_vec_env("CartPole-v1", n_envs=8) # A2C 通常使用更多并行环境

# 2. 定义 A2C 模型
# A2C 使用 "MlpPolicy" 或 "CnnPolicy"
# 关键超参数:
# n_steps: 每个环境在更新前运行多少步 (影响 TD 估计的长度)
# vf_coef: 值函数损失的系数 (Critic loss weight)
# ent_coef: 熵正则化系数 (鼓励探索)
model = A2C("MlpPolicy", vec_env, verbose=1,
            gamma=0.99,             # 折扣因子
            n_steps=5,              # 每个环境更新前运行 5 步
            vf_coef=0.5,            # 值函数损失系数
            ent_coef=0.0,           # 熵正则化系数 (CartPole 通常不需要太多探索)
            learning_rate=7e-4,     # 学习率 (A2C 通常用稍高一点的学习率)
            tensorboard_log=log_dir
           )

# 3. 训练模型
print("Starting A2C training on CartPole...")
start_time = time.time()
model.learn(total_timesteps=100000, log_interval=50) # 训练步数与 DQN 保持一致
end_time = time.time()
print(f"Training finished in {end_time - start_time:.2f} seconds.")

# 4. 保存模型
model_path = os.path.join(log_dir, "a2c_cartpole_sb3")
model.save(model_path)
print(f"Model saved to {model_path}.zip")

# 5. 评估训练好的模型
print("Evaluating trained A2C model...")
eval_env = gym.make("CartPole-v1")
mean_reward, std_reward = evaluate_policy(model, eval_env, n_eval_episodes=20, deterministic=True)
print(f"Evaluation results (A2C): Mean reward = {mean_reward:.2f} +/- {std_reward:.2f}")

vec_env.close()
eval_env.close()

print(f"To view training logs, run: tensorboard --logdir {log_dir}")

# --- (可选) 运行 A2C on Pendulum-v1 ---
# print("\nStarting A2C training on Pendulum...")
# log_dir_pendulum = "/tmp/gym_a2c_pendulum/"
# os.makedirs(log_dir_pendulum, exist_ok=True)
# vec_env_pendulum = make_vec_env("Pendulum-v1", n_envs=8)
# model_pendulum = A2C("MlpPolicy", vec_env_pendulum, verbose=1,
#                      gamma=0.99,
#                      n_steps=5,
#                      vf_coef=0.5,
#                      ent_coef=0.0, # Pendulum 可能需要一点熵正则化
#                      learning_rate=7e-4,
#                      tensorboard_log=log_dir_pendulum
#                     )
# start_time = time.time()
# model_pendulum.learn(total_timesteps=200000, log_interval=50) # Pendulum 可能需要更多步数
# end_time = time.time()
# print(f"Pendulum training finished in {end_time - start_time:.2f} seconds.")
# model_path_pendulum = os.path.join(log_dir_pendulum, "a2c_pendulum_sb3")
# model_pendulum.save(model_path_pendulum)
# print(f"Pendulum model saved to {model_path_pendulum}.zip")

# print("Evaluating trained A2C model on Pendulum...")
# eval_env_pendulum = gym.make("Pendulum-v1")
# mean_reward_p, std_reward_p = evaluate_policy(model_pendulum, eval_env_pendulum, n_eval_episodes=10, deterministic=True)
# print(f"Evaluation results (A2C on Pendulum): Mean reward = {mean_reward_p:.2f} +/- {std_reward_p:.2f}")
# vec_env_pendulum.close()
# eval_env_pendulum.close()
# print(f"To view Pendulum training logs, run: tensorboard --logdir {log_dir_pendulum}")

网络结构详解 (默认 MlpPolicy)

在上面的示例代码中，我们使用了 A2C("MlpPolicy", vec_env, ...)。这里的 "MlpPolicy" 是 Stable Baselines3 (SB3) 提供的一个预定义策略，它为 Actor-Critic 架构构建了基于多层感知机 (Multi-Layer Perceptron, MLP) 的神经网络。虽然代码中没有显式定义每一层的具体参数，但 MlpPolicy 会使用一套标准的默认配置。

通用结构:

• 输入层 (Input Layer): 接收环境的状态观测值。
• 隐藏层 (Hidden Layers): Actor (策略网络) 和 Critic (价值网络) 通常各自拥有独立的隐藏层。对于 MlpPolicy，SB3 的默认配置通常是：
  • 网络结构 (net_arch): [dict(pi=[64, 64], vf=[64, 64])]。这意味着 Actor (pi) 和 Critic (vf) 各自有两个包含64个神经单元的隐藏层。
  • 激活函数 (activation_fn): 默认使用 Tanh 作为隐藏层的激活函数。
• 输出层 (Output Layer):
  • Actor 网络: 输出动作或动作的参数。
  • Critic 网络: 输出状态的价值估计。

1. CartPole-v1 环境 (离散动作空间)

• 状态观测 (Input): 4个连续值 (小车位置、小车速度、杆子角度、杆尖速度)。
• Actor 网络 (\(\pi(a|s, \theta)\)):
  • 输入层: 4 个单元。
  • 隐藏层 1: 64 个单元 (Tanh 激活)。
  • 隐藏层 2: 64 个单元 (Tanh 激活)。
  • 输出层: 2 个单元 (对应向左和向右两个离散动作)，之后通常连接一个 Softmax 激活函数，输出每个动作的选择概率。
• Critic 网络 (\(V(s, w)\)):
  • 输入层: 4 个单元。
  • 隐藏层 1: 64 个单元 (Tanh 激活)。
  • 隐藏层 2: 64 个单元 (Tanh 激活)。
  • 输出层: 1 个单元 (线性激活)，输出当前状态的价值估计 \(V(s)\)。

2. Pendulum-v1 环境 (连续动作空间)

• 状态观测 (Input): 3个连续值 (\(\cos(\text{杆角度})\), \(\sin(\text{杆角度})\), 杆角速度)。
• Actor 网络 (\(\pi(a|s, \theta)\)):
  • 输入层: 3 个单元。
  • 隐藏层 1: 64 个单元 (Tanh 激活)。
  • 隐藏层 2: 64 个单元 (Tanh 激活)。
  • 输出层:
    • 对于连续动作空间，Actor 网络通常输出动作分布的参数。SB3 中，对于高斯策略 (Gaussian policy)，网络会输出动作的均值 (mean)。Pendulum 环境的动作是1个连续值 (力矩)，所以输出层有1个单元代表该均值 (通常是线性激活后接一个 Tanh 来限制动作范围)。
    • 动作分布的标准差 (standard deviation) 也是学习的一部分。在 SB3 的 MlpPolicy 中，标准差（或其对数 log_std）通常是独立于状态的可学习参数，并为每个动作维度学习一个。
• Critic 网络 (\(V(s, w)\)):
  • 输入层: 3 个单元。
  • 隐藏层 1: 64 个单元 (Tanh 激活)。
  • 隐藏层 2: 64 个单元 (Tanh 激活)。
  • 输出层: 1 个单元 (线性激活)，输出当前状态的价值估计 \(V(s)\)。

如何自定义网络结构

如果你想使用不同于默认设置的网络结构，例如改变隐藏层的数量、每层的神经元数量或激活函数，可以通过在创建 A2C 模型时传递 policy_kwargs 参数来实现。

下面是一个示例，展示如何为 Actor 和 Critic 网络自定义隐藏层和激活函数：

import gymnasium as gym
from stable_baselines3 import A2C
from stable_baselines3.common.env_util import make_vec_env
from stable_baselines3.common.evaluation import evaluate_policy
import torch.nn as nn # 引入 torch.nn 来指定激活函数
import os

# 假设 log_dir 已创建
log_dir = "/tmp/gym_a2c_custom/"
os.makedirs(log_dir, exist_ok=True)

# 1. 创建环境
vec_env = make_vec_env("CartPole-v1", n_envs=4)

# 2. 定义自定义网络结构的参数
# policy_kwargs 接受一个字典
# net_arch: 定义 Actor (pi) 和 Critic (vf) 的网络层结构
#   例如 [128, 128] 表示两个包含128个单元的隐藏层
# activation_fn: 指定激活函数，例如 nn.ReLU, nn.Tanh, nn.ELU
policy_kwargs = dict(
    net_arch=dict(pi=[128, 64], vf=[128, 64]), # Actor 和 Critic 各自两层，神经元数分别为 128, 64
    activation_fn=nn.ReLU                     # 使用 ReLU 作为激活函数
)

# 3. 定义 A2C 模型，并传入 policy_kwargs
model_custom = A2C(
    "MlpPolicy",
    vec_env,
    verbose=1,
    policy_kwargs=policy_kwargs, # 应用自定义网络结构
    gamma=0.99,
    n_steps=5,
    vf_coef=0.5,
    ent_coef=0.0,
    learning_rate=7e-4,
    tensorboard_log=log_dir
)

# 4. 训练模型
print("Starting A2C training on CartPole with custom network...")
model_custom.learn(total_timesteps=50000, log_interval=50) # 训练少量步数作为演示
print("Custom training finished.")

# (可选) 打印模型结构来查看 Actor 和 Critic 的网络
# 注意：这会打印出 PyTorch 模块的详细信息
# print("Actor's network architecture:")
# print(model_custom.policy.mlp_extractor.policy_net)
# print("\nCritic's network architecture:")
# print(model_custom.policy.mlp_extractor.value_net)

# 5. 保存和评估 (与之前类似)
model_path_custom = os.path.join(log_dir, "a2c_cartpole_custom_sb3")
model_custom.save(model_path_custom)
print(f"Custom model saved to {model_path_custom}.zip")

eval_env_custom = gym.make("CartPole-v1")
mean_reward_custom, std_reward_custom = evaluate_policy(model_custom, eval_env_custom, n_eval_episodes=10)
print(f"Evaluation results (Custom A2C): Mean reward = {mean_reward_custom:.2f} +/- {std_reward_custom:.2f}")

vec_env.close()
eval_env_custom.close()
print(f"To view custom training logs, run: tensorboard --logdir {log_dir}")

解释 policy_kwargs:

• net_arch:
  • 你可以为 Actor (pi) 和 Critic (vf) 指定不同的结构。例如 dict(pi=[256, 128], vf=[64, 64])。
  • 如果共享层，可以这样定义：[64, 64, dict(pi=[32], vf=[32])]，表示先有两个共享的64单元层，然后 Actor 和 Critic 各自有一个32单元的输出前一层。但对于 A2C 的 MlpPolicy，通常 pi 和 vf 是独立的路径。
• activation_fn: 可以从 torch.nn 模块中选择不同的激活函数，如 nn.ReLU, nn.Tanh, nn.LeakyReLU, nn.ELU 等。

通过这种方式，你可以更灵活地调整模型结构以适应不同任务的复杂性。

任务与思考

1. 运行 A2C on CartPole: 运行代码的前半部分（CartPole）。使用 TensorBoard 观察训练曲线 (rollout/ep_rew_mean)。查看最终的评估结果。
2. 对比 A2C 与 DQN (CartPole):
   • 比较 A2C 和上周 DQN 在 CartPole 上的收敛速度（达到相似性能所需的步数）和最终性能（评估奖励）。哪个表现更好或更快？（注意：超参数可能需要调整才能公平比较）。
   • 考虑两种算法的样本效率。哪个算法似乎需要更少的交互步数来学习？（提示：DQN 使用经验回放，A2C 通常是 On-Policy）。
3. (可选) 运行 A2C on Pendulum: 取消注释代码的后半部分，运行 A2C 解决 Pendulum-v1 问题。观察训练曲线和评估结果。思考为什么 DQN 无法直接用于此任务，而 A2C 可以？
4. 分析 Actor-Critic:
   • 解释 Actor-Critic 框架如何结合策略学习和价值学习。
   • Critic 在 Actor-Critic 中扮演什么角色？它如何帮助 Actor 学习？
   • 什么是优势函数？为什么在策略梯度更新中使用优势函数估计（如 TD 误差）通常比使用原始回报更好？