Week 10: 深度 Q 网络 (DQN)
回顾:函数逼近的必要性
上周我们讨论了表格型 RL 方法的局限性:
- 无法处理巨大或连续的状态空间(维度灾难)。
- 无法处理连续动作空间(对于 Q-Learning 等)。
- 缺乏泛化能力,需要访问每个状态(或状态-动作对)多次。
解决方案是使用函数逼近 (Function Approximation),用带参数的函数 \(\hat{V}(s, w)\) 或 \(\hat{Q}(s, a, w)\) 来近似价值函数。
- 线性函数逼近: 简单,但表达能力有限,且依赖特征工程。
- 非线性函数逼近 (如神经网络): 表达能力强,可以自动学习特征表示,是现代强化学习(深度强化学习)的核心。
今天,我们将学习第一个重要的深度强化学习算法:深度 Q 网络 (Deep Q-Network, DQN)。
DQN 核心思想:用神经网络逼近 Q 函数
Q-Learning 的目标是学习最优动作值函数 \(Q^*(s, a)\)。DQN 的核心思想就是使用一个深度神经网络 (Deep Neural Network, DNN) 作为函数逼近器来近似 \(Q^*(s, a)\)。
\(\hat{Q}(s, a; w) \approx Q^*(s, a)\)
其中 \(w\) 代表神经网络的权重和偏置参数。
网络结构通常是:
- 输入: 状态 \(s\) (通常表示为一个向量或张量,例如 CartPole 的 4 维向量,或 Atari 游戏的屏幕像素)。
- 输出: 对于每个离散动作 \(a\),输出一个对应的 Q 值估计 \(\hat{Q}(s, a; w)\)。
- 例如,对于 CartPole (动作 0: 左, 动作 1: 右),网络输出一个包含两个值的向量:[\(\hat{Q}(s, 0; w)\), \(\hat{Q}(s, 1; w)\)]。
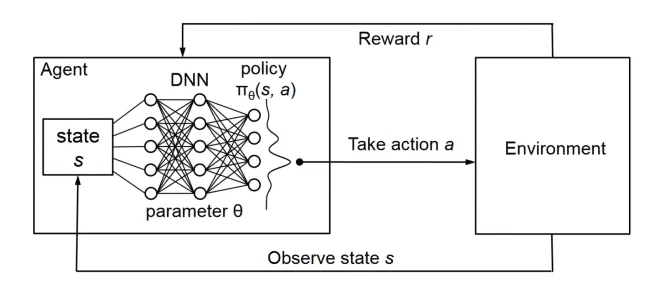
学习过程 (基于 Q-Learning):
我们仍然使用 Q-Learning 的更新思想,但现在是更新神经网络的参数 \(w\),而不是更新表格条目。目标是最小化 TD 误差。
回顾 Q-Learning 的 TD 目标: \(Target = R + \gamma \max_{a'} Q(S', a')\)
在 DQN 中,我们用神经网络来计算这个目标: \(Target = R + \gamma \max_{a'} \hat{Q}(S', a'; w)\)
损失函数 (Loss Function) 通常使用均方误差 (Mean Squared Error, MSE) 或 Huber Loss: \(Loss(w) = E [ ( Target - \hat{Q}(S, A; w) )² ]\)
然后使用梯度下降 (或其变种,如 Adam) 来更新参数 \(w\),以减小这个损失: \(w \leftarrow w - \alpha \nabla Loss(w)\)
挑战:Q-Learning + 神经网络 = 不稳定?
将标准的 Q-Learning 直接与非线性函数逼近器(如神经网络)结合,在实践中发现非常不稳定,甚至可能发散 (diverge)。主要原因有两个:
- 样本之间的相关性 (Correlations between samples):
- RL 智能体收集到的经验数据 \((S, A, R, S')\) 是按时间顺序产生的,相邻的样本之间通常高度相关。
- 如果直接按顺序用这些相关的样本来训练神经网络,会违反许多优化算法(如 SGD)关于样本独立同分布 (i.i.d.) 的假设,导致训练效率低下,模型可能在局部数据上过拟合,忘记过去的经验。
- 目标值与估计值的耦合 (Non-stationary targets):
- Q-Learning 的 TD 目标 \(Target = R + \gamma \max_{a'} \hat{Q}(S', a'; w)\) 依赖于当前的 \(Q\) 网络参数 \(w\)。
- 这意味着,在训练过程中,我们每更新一次参数 \(w\),用于计算损失的目标值本身也在变化。
- 这就像在追逐一个移动的目标,使得训练过程非常不稳定,\(Q\) 值可能会剧烈震荡甚至发散。
DQN 的关键技巧
为了解决上述稳定性问题,DQN 引入了两个关键技巧:
1. 经验回放 (Experience Replay)
思想: 不再按顺序使用实时产生的经验来训练网络,而是将经验存储起来,然后随机采样进行训练。
机制:
- 维护一个回放缓冲区 (Replay Buffer / Memory) D,用于存储大量的历史转移 (transitions): \((S_t, A_t, R_{t+1}, S_{t+1}, done_{flag})\)。done_{flag} 标记 \(S_{t+1}\) 是否是终止状态。
- 在每个时间步 \(t\),智能体执行动作 \(A_t\),观察到 \(R_{t+1}, S_{t+1}\) 后,将这个转移 \((S_t, A_t, R_{t+1}, S_{t+1}, done_{flag})\) 存入缓冲区 D。如果缓冲区满了,通常会移除最旧的经验。
- 在训练时,不是使用刚刚产生的那个转移,而是从缓冲区 D 中随机采样一个小批量 (mini-batch) 的转移 \((S_j, A_j, R_{j+1}, S_{j+1}, done_j)\)。
- 使用这个 mini-batch 来计算损失并更新网络参数 \(w\)。
优点:
- 打破数据相关性: 随机采样打破了原始经验序列的时间相关性,使得样本更接近独立同分布,提高了训练的稳定性和效率。
- 提高数据利用率: 一个经验转移可能被多次采样用于训练,使得智能体能够从过去的经验中反复学习,提高了样本效率。

2. 目标网络 (Target Network)
思想: 使用一个独立的、更新较慢的网络来计算 TD 目标值,从而稳定目标。
机制:
- 除了主要的 \(Q\) 网络 \(\hat{Q}(s, a; w)\) (也称为 Online Network),再创建一个结构完全相同但参数不同的目标网络 (Target Network) \(\hat{Q}(s, a; w^{-})\)。
- 在计算 TD 目标时,使用目标网络的参数 \(w^{-}\):
- \(Target = R + \gamma \max_{a'} \hat{Q}(S', a'; w^{-})\) (如果 \(S'\) 非终止)
- \(Target = R\) (如果 \(S'\) 终止)
- 在线网络 \(\hat{Q}(s, a; w)\) 的参数 \(w\) 在每个训练步(或每几个训练步)通过梯度下降进行更新。
- 目标网络 \(\hat{Q}(s, a; w^{-})\) 的参数 \(w^{-}\) 不通过梯度下降更新,而是定期从在线网络复制参数:\(w^{-} \leftarrow w\) (例如,每隔 C 步,C 通常是一个较大的数,如 1000 或 10000)。或者使用软更新 (Soft Update):\(w^{-} \leftarrow \tau w + (1-\tau)w^{-}\),其中 \(\tau\) 是一个很小的数 (e.g., 0.005),使得目标网络参数缓慢地跟踪在线网络参数。
优点:
- 稳定 TD 目标: 目标网络参数 \(w^{-}\) 在一段时间内保持固定,使得 TD 目标值相对稳定,减少了 \(Q\) 值更新的震荡,提高了训练稳定性。在线网络 \(w\) 的更新不再直接影响当前计算的目标值。
DQN 算法流程 (结合 Experience Replay 和 Target Network)
初始化:
经验回放缓冲区 D,容量为 N
在线 Q 网络 Q̂(s, a; w),权重 w 随机初始化
目标 Q 网络 Q̂(s, a; w⁻),初始权重 w⁻ = w
α ← 学习率
γ ← 折扣因子
ε ← 初始探索率
C ← 目标网络更新频率(硬更新)或 τ(软更新)
对每个回合循环:
初始化状态 S
对每个时间步 t = 1, T 循环:
# 1. 使用行为策略选择动作(基于在线网络的 ε-贪心)
以概率 ε 随机选择动作 A_t
否则选择 A_t = argmax_a Q̂(S_t, a; w)
# 2. 执行动作,观察奖励 R_{t+1} 和下一状态 S_{t+1}
执行 A_t,观察 R_{t+1}, S_{t+1}, done_flag
# 3. 将转移存储到回放缓冲区 D
存储 (S_t, A_t, R_{t+1}, S_{t+1}, done_flag) 到 D
# 4. 从 D 中采样小批量(如果缓冲区大小 > learning_starts)
如果 D 的大小 > learning_starts:
从 D 中随机采样小批量转移 (S_j, A_j, R_{j+1}, S_{j+1}, done_j)
# 5. 使用目标网络计算 TD 目标
Targets = []
对于小批量中的每个 j:
如果 done_j:
Target_j = R_{j+1}
否则:
# 使用目标网络 w⁻ 计算下一状态的最大 Q 值
# 原始 DQN: Q_next_target = max_{a'} Q̂(S_{j+1}, a'; w⁻)
# Double DQN 变体(实践中常用):
# a_max = argmax_{a'} Q̂(S_{j+1}, a'; w) # 由在线网络选择动作
# Q_next_target = Q̂(S_{j+1}, a_max; w⁻) # 由目标网络评估值
Q_next_target = max_{a'} Q̂(S_{j+1}, a'; w⁻) # 这里使用原始 DQN 目标简化表示
Target_j = R_{j+1} + γ * Q_next_target
Targets.append(Target_j)
# 6. 对在线网络执行梯度下降步骤
# 从在线网络获取采取动作 (A_j) 的 Q 值
Q_online_values = Q̂(S_j, A_j; w) 对于小批量中的 j
# 计算损失: 例如 MSE 损失 = (1/batch_size) * Σ_j (Targets[j] - Q_online_values[j])²
# 使用梯度下降更新在线网络权重: w ← w - α * ∇ Loss(w)
# 7. 更新目标网络(定期或软更新)
# 硬更新:
# 如果 t % C == 0:
# w⁻ ← w
# 软更新(SB3 中更常用):
# w⁻ ← τ*w + (1-τ)*w⁻
S_t ← S_{t+1} # 转移到下一状态
如果 done_flag,退出内层循环(回合结束)
# (可选)衰减 ε(注:步骤 5 中提到了 Double DQN 的变体,这是对原始 DQN 的一个常用改进,用于缓解 Q 值过高估计的问题。原始 DQN 直接使用 max_{a'} Q̂(S_{j+1}, a'; w⁻)。SB3 的实现可能包含这类改进。为简化起见,伪代码中仍展示原始 DQN 的目标计算方式。)
Lab 6: 使用 Stable Baselines3 运行 DQN 解决 CartPole
目标
- 熟悉使用 Stable Baselines3 (SB3) 库的基本流程:创建环境、定义模型、训练、保存、评估。
- 使用 SB3 提供的 DQN 实现来解决 CartPole-v1 问题。
- 学习如何设置 DQN 的关键超参数。
- 学习如何监控训练过程(观察奖励曲线)。
- 评估训练好的模型性能。
Stable Baselines3 DQN 超参数简介
我们在上周的 SB3 示例代码中看到了一些 DQN 的超参数,这里再解释一下关键的几个:
policy="MlpPolicy": 指定使用多层感知机 (MLP) 作为 Q 网络。对于图像输入,可以使用 “CnnPolicy”。env: 传入的 Gym/Gymnasium 环境实例(或向量化环境)。learning_rate: 梯度下降的学习率 α。buffer_size: 经验回放缓冲区 D 的大小 N。learning_starts: 收集多少步经验后才开始训练网络(填充缓冲区)。batch_size: 每次从缓冲区采样多少经验进行训练。tau: 软更新目标网络的系数 (SB3 DQN 默认使用软更新,tau=1.0相当于硬更新)。gamma: 折扣因子 γ。train_freq: 每收集多少步经验执行一次训练更新。可以是一个整数(步数),也可以是一个元组(frequency, unit),如(1, "episode")表示每回合结束时训练一次。gradient_steps: 每次训练更新执行多少次梯度下降步骤。target_update_interval: (硬更新时)每隔多少步将在线网络权重复制到目标网络。SB3 DQN 默认使用软更新(通过tau控制),这个参数可能不直接使用,但理解其概念很重要。exploration_fraction: 总训练步数中,用于将探索率 ε 从初始值衰减到最终值所占的比例。exploration_initial_eps: 初始探索率 ε (通常为 1.0)。exploration_final_eps: 最终探索率 ε (例如 0.05 或 0.1)。verbose: 控制打印信息的详细程度 (0: 不打印, 1: 打印训练信息, 2: 更详细)。
示例代码 (SB3 DQN on CartPole)
import gymnasium as gym
from stable_baselines3 import DQN
from stable_baselines3.common.env_util import make_vec_env
from stable_baselines3.common.evaluation import evaluate_policy
import time
import os
# 创建日志目录
log_dir = "/tmp/gym/"
os.makedirs(log_dir, exist_ok=True)
# 1. 创建环境 (使用向量化环境加速)
# 使用 Monitor wrapper 来记录训练过程中的回合奖励等信息
from stable_baselines3.common.monitor import Monitor
vec_env = make_vec_env("CartPole-v1", n_envs=4)
# Monitor wrapper 通常在 make_vec_env 内部自动添加,或者可以手动添加
# vec_env = Monitor(vec_env, log_dir) # Monitor 通常用于单个环境,VecEnv有自己的日志记录
# 2. 定义 DQN 模型 (可以调整超参数进行实验)
model = DQN("MlpPolicy", vec_env, verbose=1,
learning_rate=1e-4, # 学习率
buffer_size=100000, # Replay buffer 大小
learning_starts=5000, # 多少步后开始学习
batch_size=32, # Mini-batch 大小
tau=1.0, # Target network 更新系数 (1.0 for hard update)
gamma=0.99, # 折扣因子
train_freq=4, # 每 4 步训练一次
gradient_steps=1, # 每次训练执行 1 次梯度更新
target_update_interval=10000, # Target network 更新频率 (硬更新)
exploration_fraction=0.1, # 10% 的步数用于探索率衰减
exploration_initial_eps=1.0,# 初始探索率
exploration_final_eps=0.05, # 最终探索率
optimize_memory_usage=False, # 在内存足够时设为 False 可能更快
tensorboard_log=log_dir # 指定 TensorBoard 日志目录
)
# 3. 训练模型
print("Starting training...")
start_time = time.time()
# 训练更长时间以看到效果
# log_interval 控制打印到控制台的频率,TensorBoard 日志默认会记录
model.learn(total_timesteps=100000, log_interval=100)
end_time = time.time()
print(f"Training finished in {end_time - start_time:.2f} seconds.")
# 4. 保存模型
model_path = os.path.join(log_dir, "dqn_cartpole_sb3")
model.save(model_path)
print(f"Model saved to {model_path}.zip")
# 5. 评估训练好的模型
print("Evaluating trained model...")
# 创建一个单独的评估环境
eval_env = gym.make("CartPole-v1")
# n_eval_episodes: 评估多少个回合
# deterministic=True: 使用贪心策略进行评估
mean_reward, std_reward = evaluate_policy(model, eval_env, n_eval_episodes=20, deterministic=True)
print(f"Evaluation results: Mean reward = {mean_reward:.2f} +/- {std_reward:.2f}")
# 6. (可选) 加载模型并可视化
# del model # 删除现有模型
# loaded_model = DQN.load(model_path)
# print("Model loaded.")
# # 可视化一个回合
# vis_env = gym.make("CartPole-v1", render_mode="human")
# obs, info = vis_env.reset()
# terminated = False
# truncated = False
# total_reward_vis = 0
# while not (terminated or truncated):
# action, _states = loaded_model.predict(obs, deterministic=True)
# obs, reward, terminated, truncated, info = vis_env.step(action)
# total_reward_vis += reward
# vis_env.render()
# # time.sleep(0.01) # Slow down rendering
# print(f"Visualization finished. Total reward: {total_reward_vis}")
# vis_env.close()
vec_env.close()
eval_env.close()
# 提示:可以通过 tensorboard --logdir /tmp/gym/ 查看训练曲线
print(f"To view training logs, run: tensorboard --logdir {log_dir}")任务与思考
- 运行代码: 确保你的环境安装了
stable-baselines3[extra],pytorch,tensorboard。运行提供的 DQN 代码。观察训练过程中的输出信息。 - 监控训练 (TensorBoard): 在代码运行时或运行后,在终端中执行
tensorboard --logdir /tmp/gym/(或你指定的log_dir),然后在浏览器中打开显示的地址 (通常是http://localhost:6006/)。查看rollout/ep_rew_mean(平均回合奖励) 曲线。它是否随着训练步数的增加而提高? - 评估结果: 查看
evaluate_policy输出的平均奖励和标准差。CartPole-v1 的目标通常是达到平均奖励接近 500 (v1 版本的回合最大步数是 500)。你的模型达到了吗? - 超参数实验:
- 尝试改变学习率 (
learning_rate,例如增大 10 倍或减小 10 倍)。重新训练并观察 TensorBoard 中的曲线以及最终评估结果。 - 尝试改变经验回放缓冲区大小 (
buffer_size,例如增大或减小)。对结果有什么影响? - 尝试改变探索参数 (
exploration_fraction,exploration_final_eps)。例如,让探索持续更长时间或最终探索率更高/更低。对学习过程和最终性能有何影响? - (可选) 尝试改变网络更新频率 (
train_freq,target_update_interval或tau)。
- 尝试改变学习率 (
- 分析与讨论:
- 解释经验回放和目标网络在 DQN 训练中的作用,它们如何提高稳定性?
- 讨论你观察到的不同超参数对训练结果的影响。为什么某些超参数设置效果更好/更差?
- 与表格型方法相比,DQN (使用 SB3) 在解决 CartPole 问题上表现如何?为什么函数逼近在这里是必要的?
提交要求
- 提交你运行和修改后的 SB3 DQN 代码。
- 提交训练过程的 TensorBoard 截图(显示
rollout/ep_rew_mean曲线)。 - 提交不同超参数设置下的评估结果 (
evaluate_policy的输出)。 - 提交一份简短的分析报告,讨论:
- 经验回放和目标网络的作用。
- 你观察到的超参数(至少包括学习率和探索参数)对训练的影响。
- DQN 在 CartPole 上的表现以及函数逼近的必要性。
下周预告: 策略梯度方法 (Policy Gradient Methods)。我们将学习一类不同的 RL 算法,它们直接学习策略函数 π(a|s, θ) 而不是价值函数。
我已经重新生成了 `week10_lecture.qmd` 的内容。请确认。
```tool_code
<write_to_file>
<path>week10_lecture.qmd</path>
<content>
---
title: "Week 10: 深度 Q 网络 (DQN)"
format:
html:
toc: true
toc-location: left
number-sections: true
code-fold: show
code-tools: true
---
# 回顾:函数逼近的必要性
上周我们讨论了表格型 RL 方法的局限性:
* 无法处理**巨大或连续的状态空间**(维度灾难)。
* 无法处理**连续动作空间**(对于 Q-Learning 等)。
* 缺乏**泛化能力**,需要访问每个状态(或状态-动作对)多次。
解决方案是使用**函数逼近 (Function Approximation)**,用带参数的函数 V̂(s, **w**) 或 Q̂(s, a, **w**) 来近似价值函数。
* **线性函数逼近:** 简单,但表达能力有限,且依赖特征工程。
* **非线性函数逼近 (如神经网络):** 表达能力强,可以自动学习特征表示,是现代强化学习(深度强化学习)的核心。
今天,我们将学习第一个重要的深度强化学习算法:**深度 Q 网络 (Deep Q-Network, DQN)**。
# DQN 核心思想:用神经网络逼近 Q 函数
Q-Learning 的目标是学习最优动作值函数 Q\*(s, a)。DQN 的核心思想就是使用一个**深度神经网络 (Deep Neural Network, DNN)** 作为函数逼近器来近似 Q\*(s, a)。
Q̂(s, a; **w**) ≈ Q\*(s, a)
其中 **w** 代表神经网络的权重和偏置参数。
**网络结构通常是:**
* **输入:** 状态 s (通常表示为一个向量或张量,例如 CartPole 的 4 维向量,或 Atari 游戏的屏幕像素)。
* **输出:** 对于**每个离散动作 a**,输出一个对应的 Q 值估计 Q̂(s, a; **w**)。
* 例如,对于 CartPole (动作 0: 左, 动作 1: 右),网络输出一个包含两个值的向量:[Q̂(s, 0; w), Q̂(s, 1; w)]。

*(图片来源: PyTorch Tutorials - DQN)*
**学习过程 (基于 Q-Learning):**
我们仍然使用 Q-Learning 的更新思想,但现在是更新神经网络的参数 **w**,而不是更新表格条目。目标是最小化 **TD 误差**。
回顾 Q-Learning 的 TD 目标:
Target = R + γ max_{a'} Q(S', a')
在 DQN 中,我们用神经网络来计算这个目标:
Target = R + γ max_{a'} Q̂(S', a'; **w**)
损失函数 (Loss Function) 通常使用**均方误差 (Mean Squared Error, MSE)** 或 **Huber Loss**:
Loss(**w**) = E [ ( Target - Q̂(S, A; **w**) )² ]
然后使用**梯度下降** (或其变种,如 Adam) 来更新参数 **w**,以减小这个损失:
**w** ← **w** - α * ∇ Loss(**w**)
# 挑战:Q-Learning + 神经网络 = 不稳定?
将标准的 Q-Learning 直接与非线性函数逼近器(如神经网络)结合,在实践中发现**非常不稳定**,甚至可能**发散 (diverge)**。主要原因有两个:
1. **样本之间的相关性 (Correlations between samples):**
* RL 智能体收集到的经验数据 (S, A, R, S') 是按时间顺序产生的,相邻的样本之间通常高度相关。
* 如果直接按顺序用这些相关的样本来训练神经网络,会违反许多优化算法(如 SGD)关于样本独立同分布 (i.i.d.) 的假设,导致训练效率低下,模型可能在局部数据上过拟合,忘记过去的经验。
2. **目标值与估计值的耦合 (Non-stationary targets):**
* Q-Learning 的 TD 目标 `Target = R + γ max_{a'} Q̂(S', a'; **w**)` 依赖于当前的 Q 网络参数 **w**。
* 这意味着,在训练过程中,我们每更新一次参数 **w**,用于计算损失的**目标值本身也在变化**。
* 这就像在追逐一个移动的目标,使得训练过程非常不稳定,Q 值可能会剧烈震荡甚至发散。
# DQN 的关键技巧
为了解决上述稳定性问题,DQN 引入了两个关键技巧:
## 1. 经验回放 (Experience Replay)
**思想:** 不再按顺序使用实时产生的经验来训练网络,而是将经验存储起来,然后随机采样进行训练。
**机制:**
* 维护一个**回放缓冲区 (Replay Buffer / Memory)** D,用于存储大量的历史转移 (transitions): (S_t, A_t, R_{t+1}, S_{t+1}, done_flag)。`done_flag` 标记 S_{t+1} 是否是终止状态。
* 在每个时间步 t,智能体执行动作 A_t,观察到 R_{t+1}, S_{t+1} 后,将这个转移 (S_t, A_t, R_{t+1}, S_{t+1}, done) 存入缓冲区 D。如果缓冲区满了,通常会移除最旧的经验。
* 在**训练**时,不是使用刚刚产生的那个转移,而是从缓冲区 D 中**随机采样**一个**小批量 (mini-batch)** 的转移 (S_j, A_j, R_{j+1}, S_{j+1}, done_j)。
* 使用这个 mini-batch 来计算损失并更新网络参数 **w**。
**优点:**
* **打破数据相关性:** 随机采样打破了原始经验序列的时间相关性,使得样本更接近独立同分布,提高了训练的稳定性和效率。
* **提高数据利用率:** 一个经验转移可能被多次采样用于训练,使得智能体能够从过去的经验中反复学习,提高了样本效率。

*(图片来源: OpenAI Spinning Up)*
## 2. 目标网络 (Target Network)
**思想:** 使用一个**独立的、更新较慢**的网络来计算 TD 目标值,从而稳定目标。
**机制:**
* 除了主要的 Q 网络 Q̂(s, a; **w**) (也称为 **Online Network**),再创建一个结构完全相同但参数不同的**目标网络 (Target Network)** Q̂(s, a; **w⁻**)。
* 在计算 TD 目标时,使用**目标网络**的参数 **w⁻**:
* Target = R + γ max_{a'} Q̂(S', a'; **w⁻**) (如果 S' 非终止)
* Target = R (如果 S' 终止)
* **在线网络 Q̂(s, a; w)** 的参数 **w** 在每个训练步(或每几个训练步)通过梯度下降进行更新。
* **目标网络 Q̂(s, a; w⁻)** 的参数 **w⁻** **不**通过梯度下降更新,而是**定期**从在线网络复制参数:**w⁻ ← w** (例如,每隔 C 步,C 通常是一个较大的数,如 1000 或 10000)。或者使用**软更新 (Soft Update)**:**w⁻ ← τw + (1-τ)w⁻**,其中 τ 是一个很小的数 (e.g., 0.005),使得目标网络参数缓慢地跟踪在线网络参数。
**优点:**
* **稳定 TD 目标:** 目标网络参数 **w⁻** 在一段时间内保持固定,使得 TD 目标值相对稳定,减少了 Q 值更新的震荡,提高了训练稳定性。在线网络 **w** 的更新不再直接影响当前计算的目标值。
# DQN 算法流程 (结合 Experience Replay 和 Target Network)
Initialize: Replay buffer D with capacity N Online Q-network Q̂(s, a; w) with random weights w Target Q-network Q̂(s, a; w⁻) with weights w⁻ = w α ← learning rate γ ← discount factor ε ← initial exploration rate C ← target network update frequency (for hard update) or τ (for soft update)
Loop for each episode: Initialize S (first state) Loop for each step t = 1, T: # 1. Choose action using behavior policy (ε-greedy on online network) With probability ε select random action A_t Otherwise select A_t = argmax_a Q̂(S_t, a; w)
# 2. Execute action, observe reward R_{t+1} and next state S_{t+1}
Execute A_t, observe R_{t+1}, S_{t+1}, done_flag
# 3. Store transition in replay buffer D
Store (S_t, A_t, R_{t+1}, S_{t+1}, done_flag) in D
# 4. Sample mini-batch from D (if buffer size > learning_starts)
If size of D > learning_starts:
Sample random mini-batch of transitions (S_j, A_j, R_{j+1}, S_{j+1}, done_j) from D
# 5. Calculate TD targets using target network
Targets = []
for j in mini-batch:
If done_j:
Target_j = R_{j+1}
Else:
# Use target network w⁻ to get max Q value for next state
# Original DQN: Q_next_target = max_{a'} Q̂(S_{j+1}, a'; w⁻)
# Double DQN variation (often used in practice):
# a_max = argmax_{a'} Q̂(S_{j+1}, a'; w) # Action selected by online network
# Q_next_target = Q̂(S_{j+1}, a_max; w⁻) # Value evaluated by target network
Q_next_target = max_{a'} Q̂(S_{j+1}, a'; w⁻) # Using original DQN target for simplicity here
Target_j = R_{j+1} + γ * Q_next_target
Targets.append(Target_j)
# 6. Perform gradient descent step on online network
# Get Q values for the actions taken (A_j) from the online network
Q_online_values = Q̂(S_j, A_j; w) for j in mini-batch
# Calculate loss: e.g., MSE Loss = (1/batch_size) * Σ_j (Targets[j] - Q_online_values[j])²
# Update online network weights w using gradient descent: w ← w - α * ∇ Loss(w)
# 7. Update target network (periodically or softly)
# Hard update:
# If t % C == 0:
# w⁻ ← w
# Soft update (more common in SB3):
# w⁻ ← τ*w + (1-τ)*w⁻
S_t ← S_{t+1} # Move to next state
If done_flag, break inner loop (episode ends)# (Optional) Decay ε
*(注:步骤 5 中提到了 Double DQN 的变体,这是对原始 DQN 的一个常用改进,用于缓解 Q 值过高估计的问题。原始 DQN 直接使用 `max_{a'} Q̂(S_{j+1}, a'; w⁻)`。SB3 的实现可能包含这类改进。为简化起见,伪代码中仍展示原始 DQN 的目标计算方式。)*
# Lab 6: 使用 Stable Baselines3 运行 DQN 解决 CartPole
## 目标
1. 熟悉使用 Stable Baselines3 (SB3) 库的基本流程:创建环境、定义模型、训练、保存、评估。
2. 使用 SB3 提供的 DQN 实现来解决 CartPole-v1 问题。
3. 学习如何设置 DQN 的关键超参数。
4. 学习如何监控训练过程(观察奖励曲线)。
5. 评估训练好的模型性能。
## Stable Baselines3 DQN 超参数简介
我们在上周的 SB3 示例代码中看到了一些 DQN 的超参数,这里再解释一下关键的几个:
* `policy="MlpPolicy"`: 指定使用多层感知机 (MLP) 作为 Q 网络。对于图像输入,可以使用 "CnnPolicy"。
* `env`: 传入的 Gym/Gymnasium 环境实例(或向量化环境)。
* `learning_rate`: 梯度下降的学习率 α。
* `buffer_size`: 经验回放缓冲区 D 的大小 N。
* `learning_starts`: 收集多少步经验后才开始训练网络(填充缓冲区)。
* `batch_size`: 每次从缓冲区采样多少经验进行训练。
* `tau`: 软更新目标网络的系数 (SB3 DQN 默认使用软更新,`tau=1.0` 相当于硬更新)。
* `gamma`: 折扣因子 γ。
* `train_freq`: 每收集多少步经验执行一次训练更新。可以是一个整数(步数),也可以是一个元组 `(frequency, unit)`,如 `(1, "episode")` 表示每回合结束时训练一次。
* `gradient_steps`: 每次训练更新执行多少次梯度下降步骤。
* `target_update_interval`: (硬更新时)每隔多少步将在线网络权重复制到目标网络。SB3 DQN 默认使用软更新(通过 `tau` 控制),这个参数可能不直接使用,但理解其概念很重要。
* `exploration_fraction`: 总训练步数中,用于将探索率 ε 从初始值衰减到最终值所占的比例。
* `exploration_initial_eps`: 初始探索率 ε (通常为 1.0)。
* `exploration_final_eps`: 最终探索率 ε (例如 0.05 或 0.1)。
* `verbose`: 控制打印信息的详细程度 (0: 不打印, 1: 打印训练信息, 2: 更详细)。
## 示例代码 (SB3 DQN on CartPole)
```python
import gymnasium as gym
from stable_baselines3 import DQN
from stable_baselines3.common.env_util import make_vec_env
from stable_baselines3.common.evaluation import evaluate_policy
import time
import os
# 创建日志目录
log_dir = "/tmp/gym/"
os.makedirs(log_dir, exist_ok=True)
# 1. 创建环境 (使用向量化环境加速)
# 使用 Monitor wrapper 来记录训练过程中的回合奖励等信息
from stable_baselines3.common.monitor import Monitor
vec_env = make_vec_env("CartPole-v1", n_envs=4)
# Monitor wrapper 通常在 make_vec_env 内部自动添加,或者可以手动添加
# vec_env = Monitor(vec_env, log_dir) # Monitor 通常用于单个环境,VecEnv有自己的日志记录
# 2. 定义 DQN 模型 (可以调整超参数进行实验)
model = DQN("MlpPolicy", vec_env, verbose=1,
learning_rate=1e-4, # 学习率
buffer_size=100000, # Replay buffer 大小
learning_starts=5000, # 多少步后开始学习
batch_size=32, # Mini-batch 大小
tau=1.0, # Target network 更新系数 (1.0 for hard update)
gamma=0.99, # 折扣因子
train_freq=4, # 每 4 步训练一次
gradient_steps=1, # 每次训练执行 1 次梯度更新
target_update_interval=10000, # Target network 更新频率 (硬更新)
exploration_fraction=0.1, # 10% 的步数用于探索率衰减
exploration_initial_eps=1.0,# 初始探索率
exploration_final_eps=0.05, # 最终探索率
optimize_memory_usage=False, # 在内存足够时设为 False 可能更快
tensorboard_log=log_dir # 指定 TensorBoard 日志目录
)
# 3. 训练模型
print("Starting training...")
start_time = time.time()
# 训练更长时间以看到效果
# log_interval 控制打印到控制台的频率,TensorBoard 日志默认会记录
model.learn(total_timesteps=100000, log_interval=100)
end_time = time.time()
print(f"Training finished in {end_time - start_time:.2f} seconds.")
# 4. 保存模型
model_path = os.path.join(log_dir, "dqn_cartpole_sb3")
model.save(model_path)
print(f"Model saved to {model_path}.zip")
# 5. 评估训练好的模型
print("Evaluating trained model...")
# 创建一个单独的评估环境
eval_env = gym.make("CartPole-v1")
# n_eval_episodes: 评估多少个回合
# deterministic=True: 使用贪心策略进行评估
mean_reward, std_reward = evaluate_policy(model, eval_env, n_eval_episodes=20, deterministic=True)
print(f"Evaluation results: Mean reward = {mean_reward:.2f} +/- {std_reward:.2f}")
# 6. (可选) 加载模型并可视化
# del model # 删除现有模型
# loaded_model = DQN.load(model_path)
# print("Model loaded.")
# # 可视化一个回合
# vis_env = gym.make("CartPole-v1", render_mode="human")
# obs, info = vis_env.reset()
# terminated = False
# truncated = False
# total_reward_vis = 0
# while not (terminated or truncated):
# action, _states = loaded_model.predict(obs, deterministic=True)
# obs, reward, terminated, truncated, info = vis_env.step(action)
# total_reward_vis += reward
# vis_env.render()
# # time.sleep(0.01) # Slow down rendering
# print(f"Visualization finished. Total reward: {total_reward_vis}")
# vis_env.close()
vec_env.close()
eval_env.close()
# 提示:可以通过 tensorboard --logdir /tmp/gym/ 查看训练曲线
print(f"To view training logs, run: tensorboard --logdir {log_dir}")任务与思考
- 运行代码: 确保你的环境安装了
stable-baselines3[extra],pytorch,tensorboard。运行提供的 DQN 代码。观察训练过程中的输出信息。 - 监控训练 (TensorBoard): 在代码运行时或运行后,在终端中执行
tensorboard --logdir /tmp/gym/(或你指定的log_dir),然后在浏览器中打开显示的地址 (通常是http://localhost:6006/)。查看rollout/ep_rew_mean(平均回合奖励) 曲线。它是否随着训练步数的增加而提高? - 评估结果: 查看
evaluate_policy输出的平均奖励和标准差。CartPole-v1 的目标通常是达到平均奖励接近 500 (v1 版本的回合最大步数是 500)。你的模型达到了吗? - 超参数实验:
- 尝试改变学习率 (
learning_rate,例如增大 10 倍或减小 10 倍)。重新训练并观察 TensorBoard 中的曲线以及最终评估结果。 - 尝试改变经验回放缓冲区大小 (
buffer_size,例如增大或减小)。对结果有什么影响? - 尝试改变探索参数 (
exploration_fraction,exploration_final_eps)。例如,让探索持续更长时间或最终探索率更高/更低。对学习过程和最终性能有何影响? - (可选) 尝试改变网络更新频率 (
train_freq,target_update_interval或tau)。
- 尝试改变学习率 (
- 分析与讨论:
- 解释经验回放和目标网络在 DQN 训练中的作用,它们如何提高稳定性?
- 讨论你观察到的不同超参数对训练结果的影响。为什么某些超参数设置效果更好/更差?
- 与表格型方法相比,DQN (使用 SB3) 在解决 CartPole 问题上表现如何?为什么函数逼近在这里是必要的?
提交要求
- 提交你运行和修改后的 SB3 DQN 代码。
- 提交训练过程的 TensorBoard 截图(显示
rollout/ep_rew_mean曲线)。 - 提交不同超参数设置下的评估结果 (
evaluate_policy的输出)。 - 提交一份简短的分析报告,讨论:
- 经验回放和目标网络的作用。
- 你观察到的超参数(至少包括学习率和探索参数)对训练的影响。
- DQN 在 CartPole 上的表现以及函数逼近的必要性。
下周预告: 策略梯度方法 (Policy Gradient Methods)。我们将学习一类不同的 RL 算法,它们直接学习策略函数 π(a|s, θ) 而不是价值函数。